Quantum Actuarial: Part 1—The Prelude of the Harmonic Oscillator

Quantum Harmonic Oscillator: The Spring of the Microscopic World

The quantum harmonic oscillator is one of the classic models in quantum mechanics, originating from the concept of the harmonic oscillator in classical mechanics but exhibiting unique quantum characteristics within the quantum framework. The harmonic oscillator is an ideal physical model used to describe the phenomenon of an object undergoing periodic vibration under the influence of a force. The classical simple harmonic oscillator also has many applications in other fields. In financial markets, the prices or rates of return of assets often exhibit periodic behavior similar to that of a harmonic oscillator.

From Classical to Quantum: The Transition from Determinism to Superposition States

In classical physics, the behavior of the harmonic oscillator adheres to Newton's laws of motion. This highlights the determinism and predictability of macroscopic physical laws. However, when delving into the microscopic realm, the rules of classical physics no longer apply. In the quantum realm, particles no longer follow continuous trajectories but exhibit a quantum characteristic. Similarly, the quantum harmonic oscillator is no longer a simple spring model; the particle is no longer a simple mass point but exhibits a fascinating superposition state. This means that a particle can simultaneously exist in multiple positions and states.

In the field of insurance actuarial science, actuaries deal with future events that are fraught with uncertainty, much like the uncertainty embodied by a quantum harmonic oscillator. The risks and probability distributions handled in insurance actuarial work often cannot be described by deterministic models found in classical physics; instead, they are more akin to probability wave functions in quantum mechanics, capable of existing in multiple possibilities simultaneously, only collapsing into a definite state upon the occurrence of a specific event.[1] Therefore, from this perspective, quantum concepts are better suited than those of classical physics for understanding and describing issues of uncertainty in insurance actuarial science.

The Probability Wave Distribution Characteristics of the Quantum Harmonic Oscillator

Upon entering the field of quantum mechanics, the quantum harmonic oscillator follows the Schrödinger equation, which is the fundamental equation describing the temporal evolution of quantum systems. In quantum mechanics, the state of a particle is described by a probability wave, and the distribution of this probability wave reflects the probability of the particle's presence in space. If the potential function of the environmental factors conforms to simple harmonic motion, then takes a quadratic form, which can be represented as[2, 3]

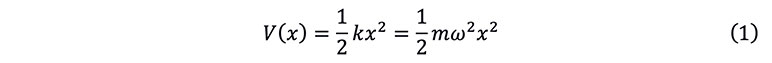
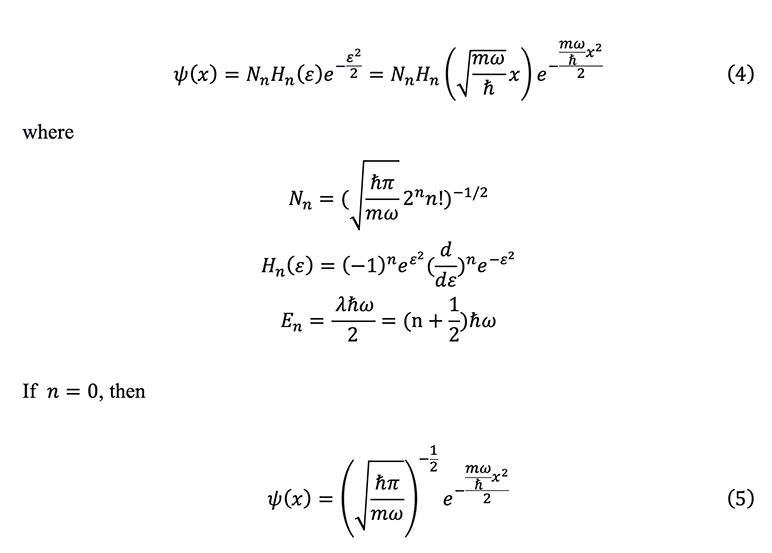
, where m is the mass of the particle, is the angular frequency of the oscillator. (See Figure 1)

Figure 1

Potential Function of a One-Dimensional Harmonic Oscillator

Substitute the potential function of the harmonic oscillator into the following Schrödinger equation

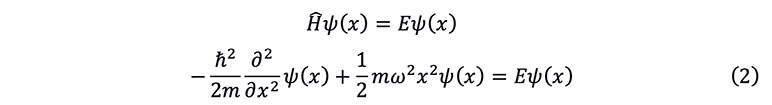
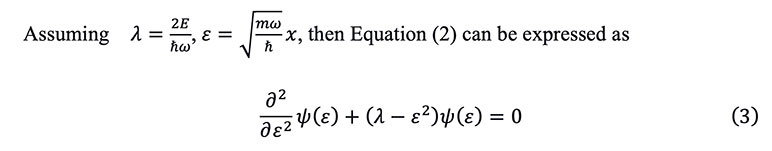
By solving the partial differential equation, the characteristic solution of Equation (3) can be expressed as

When the quantum harmonic oscillator is at its ground state , corresponds to the normal distribution function. However, when , the form of the squared magnitude of the wave function becomes more complex, composed of multiple Gaussian wave packets. These wave packets form a series of discrete wave crests and troughs in space, with each extremum representing a high probability of the particle appearing at specific locations (as shown in Figure 3). This multi-peak structure intuitively reveals the particle's distribution probability in different spatial regions and its potential for transitions between different energy levels. As the energy level increases, the frequency and likelihood of the particle transitioning between various energy levels also increase, reflecting the dynamism and instability of the system in high-energy states. (See Figure 2)

Figure 2

Energy Level Distribution of the Quantum Harmonic Oscillator

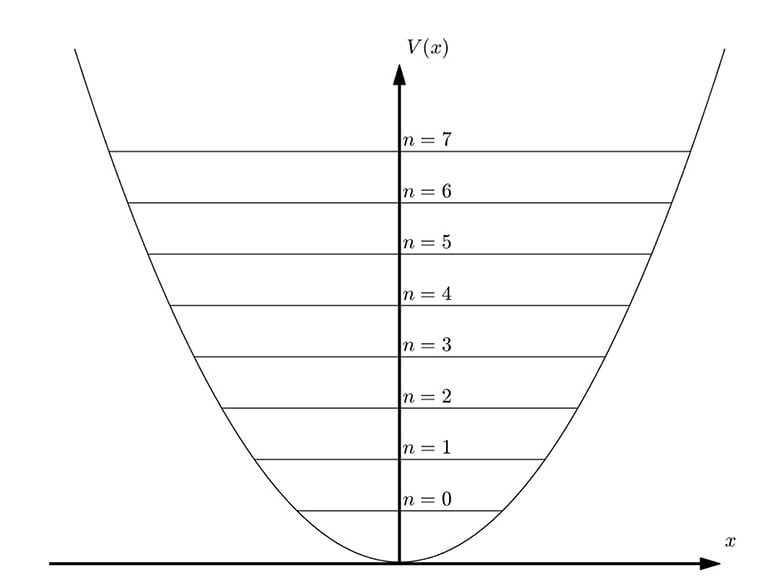
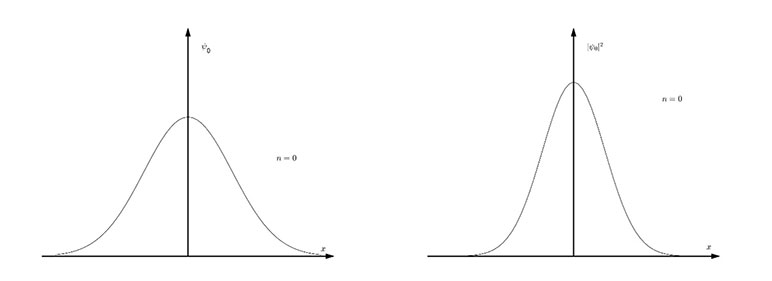
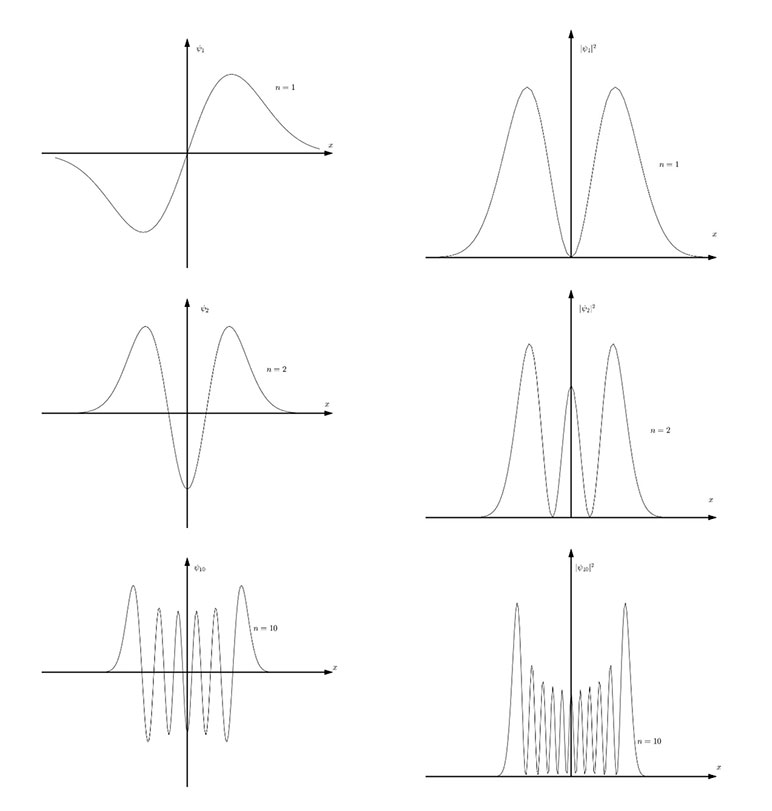
Figure 3

Wave Function and Probability Distribution Function at Different Energy Levels

Mapping to the vast field of actuarial science, the theory of the quantum harmonic oscillator reveals a unique charm. Just as the quantum simple harmonic vibration depicts the periodic conversion of energy in a potential well, the external environment in the insurance field also exhibits a similar periodic cycle of positive and negative feedback loops, with their similarity being self-evident.

The following discussion will delve into how the quantum harmonic oscillator model can be specifically integrated into the cost analysis of medical insurance and the study of interest rate patterns, revealing the hidden cyclical fluctuation patterns behind them, thereby providing a different perspective for strategy formulation and risk management in the insurance industry.

The Distribution Pattern of Medical Insurance Costs

With medical insurance, as an important means of risk transfer, the exploration of its cost distribution pattern is crucial for the stable operation of the insurance industry. Medical costs are influenced by a variety of factors such as disease type, severity, treatment choices, and individual differences, presenting complexity and diversity in their distribution. As previously mentioned, in quantum mechanics, the energy level distribution of the harmonic oscillator exhibits discrete characteristics, with each energy level corresponding to a specific energy state, and the transition of particles between energy levels follows probabilistic laws. This physical model shows a certain similarity to the distribution of medical costs in medical insurance.

The distribution characteristics of basic medical costs exhibit a stable trend. The medical consumption of the broad patient population is mainly composed of routine diagnostic and treatment services and basic drug expenses. These routine costs are frequent but maintain a relatively low level, while patients requiring high treatment costs for severe illnesses are relatively fewer. In this scenario, the distribution of medical costs will conform to the law of large numbers, following the pattern of normal distribution. The core feature is that patient medical expenses tend to gather around a central value, with large or small expenditures away from this central value significantly decreasing. This distribution is consistent with the probability wave distribution of the quantum harmonic oscillator in its ground state, and both interpret the probability density characteristics of the system when it is in a steady state. According to the analysis of medical cost distribution data in the report on the trends of commercial health insurance costs in the United States,[4] this view can be further confirmed. As shown in Figure 4, the distribution function of medical costs has a high degree of similarity with the probability wave function of the quantum harmonic oscillator at the zero-energy level. This not only provides a new perspective for understanding the statistical laws of medical costs, but also reveals the mathematical connection between microscopic particles and medical insurance.

Figure 4

Distribution of Monthly Average Compensation Amounts for Commercial Health Insurance in the United States from 2009 to 2015

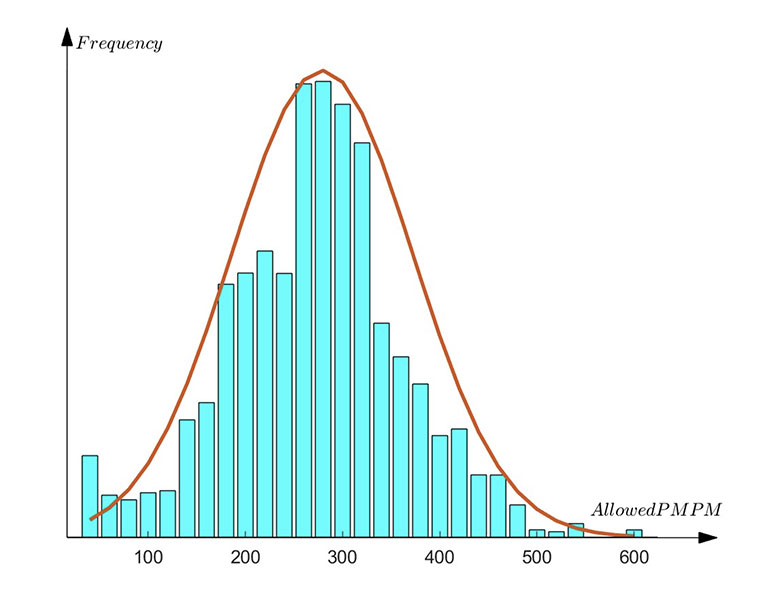
However, when it comes to the medical costs of a specific disease, in actual medical practice, according to its severity, it can be divided into different levels such as mild, moderate, and severe. The treatment methods and costs required for patients of different levels vary greatly. Therefore, under different treatment methods, the distribution of medical costs no longer presents a single normal distribution pattern but shows multiple discrete probability maxima, forming a multimodal distribution similar to that of a multi-level quantum harmonic oscillator. This discrete pattern has certain similarities with the distribution characteristics of multi-level quantum harmonic oscillators. In quantum mechanics, the energy levels of a multi-level harmonic oscillator are discrete, with each level corresponding to a specific energy value. When a particle is at a certain energy level, its probability wave distribution shows a specific pattern, with the positions of the wave peaks and troughs reflecting the probability of the particle appearing at different locations. Similarly, in medical insurance, the medical costs under different treatment methods can also be regarded as discrete energy levels, each corresponding to a specific cost range. When a patient's condition changes or the treatment effect is poor, the doctor may adjust the treatment plan, causing the medical costs to transition from one energy level to another. The process of patients receiving different treatment methods is akin to the transition of particles between different energy levels, and the distribution of medical costs shows discreteness similar to that of a probability wave.

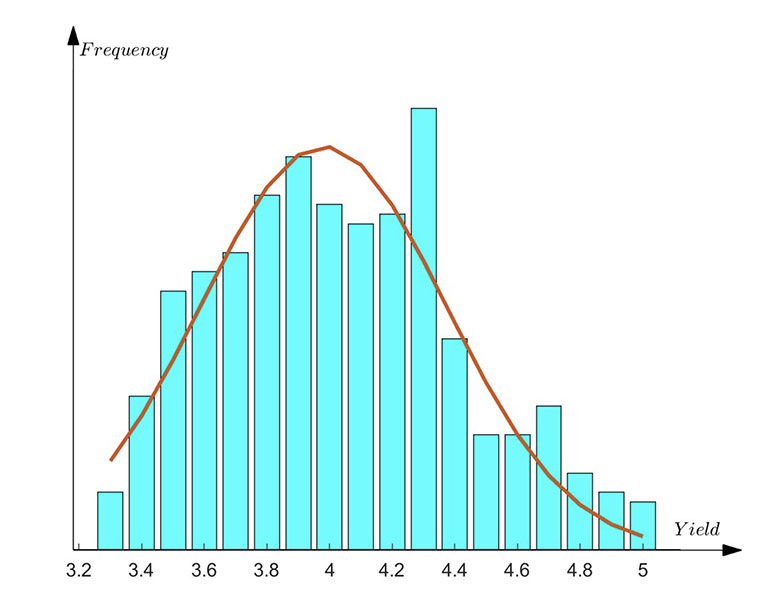
For example, according to the research results of MESA (Multi-Ethnic Study of Atherosclerosis),[5] we can gain a deeper understanding of the relationship between disease severity and medical costs. Cardiovascular disease (CVD), as a common health issue, sees its treatment costs rise significantly with increasing disease severity. In the context of CVD, this stratification is directly linked to the choice of treatment methods and their corresponding costs. For low-risk patients, their treatments are typically less costly and can be conducted in an outpatient setting. On the other hand, high-risk patients’ treatment methods are not only costly, but may also require long-term medical supervision and frequent follow-ups. There is a significant difference in the treatment methods and costs accepted by patients at different risk levels, with costs rising stepwise from basic drug therapy to innovative therapies or long-term care, forming a multimodal distribution. This indicates that in the analysis of medical insurance costs, the introduction of the quantum harmonic oscillator model can more accurately capture the discrete characteristics of the distribution of medical costs.

Therefore, as the severity of the disease increases, medical costs show an increasing trend, demonstrating that under different treatment methods, medical costs will have multiple different peaks. This phenomenon emphasizes the importance of disease prevention and management, as well as the necessity of early identification and intervention to reduce overall medical costs. Precise pricing of insurance products needs to incorporate this characteristic. By drawing on the probability calculation methods in quantum mechanics and combining with the quantum harmonic oscillator model, a more refined model of the distribution of medical insurance costs can be constructed. Through historical data analysis, the cost peaks under different treatment methods can be determined and mapped to different energy levels of the model, and then the probability of the occurrence of costs at each energy level can be calculated to obtain the probability density function of the cost distribution. This method not only improves the accuracy of cost prediction but also provides a scientific basis for identifying high-risk treatment methods.

It is worth mentioning that when a new treatment method is introduced in the market, a new peak in claims data can be observed in the short term, a phenomenon similar to the unstable state of the quantum harmonic oscillator at high energy levels. In quantum mechanics, the high-energy state of the oscillator is unstable, and particles tend to decay rapidly to lower energy levels by releasing energy to achieve a more stable energy state. The market also shows a similar adaptation process. With the introduction of new treatment methods, there may be a short-term peak in the number of claims due to information asymmetry, surge in demand, or supply constraints. However, as the market gradually adapts and evaluates the new technology, including cost-benefit analysis, evidence accumulation of treatment effects, and adjustment of supply and demand relationships, market forces will push prices and claim frequencies toward a long-term equilibrium state. Just as the quantum oscillator tends to its ground state, the medical market, after the initial fluctuations, will gradually achieve stability in prices and claims through market screening and self-regulation mechanisms. This process not only reflects market efficiency but also demonstrates the insurance industry's adaptation to medical innovation, maintenance of consumer rights, and achievement of sustainable development.

In summary, the distribution pattern of medical costs in medical insurance is influenced by a variety of factors and shows complex and changeable characteristics. When understanding and analyzing this distribution pattern, the probability wave distribution characteristics of the quantum harmonic oscillator can be used as an analogy to better understand the discreteness of medical costs in medical insurance. This analogy not only helps to build insurance actuarial pricing models that are more in line with actual situations, but also provides new ideas and methods to optimize insurance product design and risk management strategies.

The Interest Rate Pattern in Insurance Pricing and Assessment

The life insurance market is characterized by long-term operations, where pricing interest rates and investment returns are closely related to the level of interest rates. The volatility of interest rates is an important risk factor in the life insurance market, directly affecting the profitability and risk-bearing capacity of insurance companies. Therefore, the analysis and prediction of interest rate volatility are crucial tasks in actuarial science. In this context, the quantum harmonic oscillator model provides a novel and unique perspective for understanding the intrinsic laws of interest rate fluctuations.

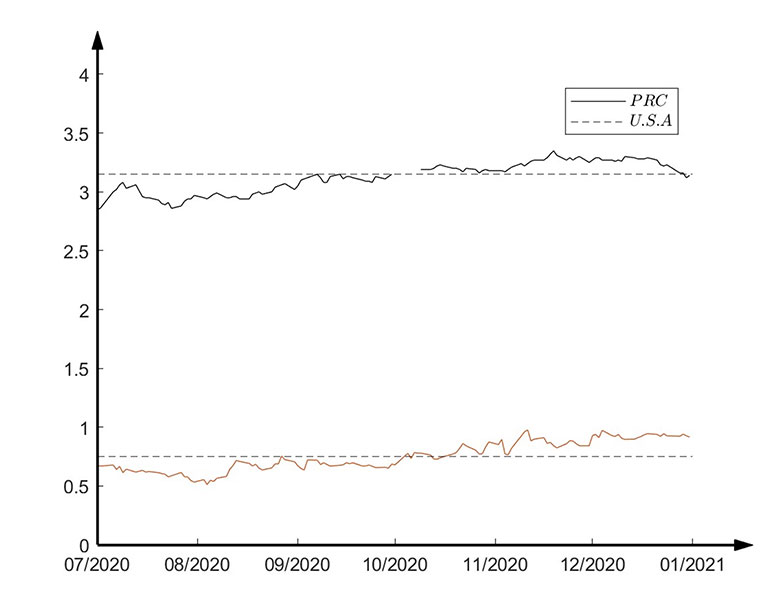
Life insurance companies typically use the spot yield of government bonds as the benchmark for assessing interest rates because it is considered one of the safest and most stable interest rate indicators in the market. In the short term, the spot yield of government bonds is influenced by supply and demand and usually fluctuates around the market's expected price. When the spot yield of government bonds is greatly deviated from the market’s expectation, it will trigger the actions of speculators. Speculators may adopt strategies of short-selling or going long on bonds, causing the yield to return to the market's expected level. As a result, the yield fluctuates around the market expectation, with a lower probability of being abnormally high/low, similar to the normal distribution state of the quantum harmonic oscillator at the ground state, as shown in Figure 5. This assumption and concept are similar to classical interest rate models, such as Vasicek, Hull-White, CIR, etc.

Figure 5

U.S. 10-Year Treasury Yield from June 2020 to April 2024

In a longer time horizon, interest rates are primarily driven by the stage of macroeconomic development. In the past years, developed countries have had a higher level of economic development, more sophisticated financial markets, and greater efficiency in the circulation of capital. Coupled with relatively lower economic growth rates, the financing costs are naturally not high, hence their interest rates tend to stabilize at a lower level. In contrast, developing countries have more robust consumption and investment demands, requiring a larger amount of capital, but with relatively less developed financing channels, leading to interest rates that are concentrated at a higher level. This phenomenon of interest rates stabilizing at different levels depending on the development stage is similar to the multi-peak distribution of a multi-level quantum harmonic oscillator. As shown in Figure 6, the Chinese 10-year government bond yield and the U.S. 10-year Treasury yield are stable at different levels.

Figure 6

2020 U.S.—China 10-Year Government Bond Yields

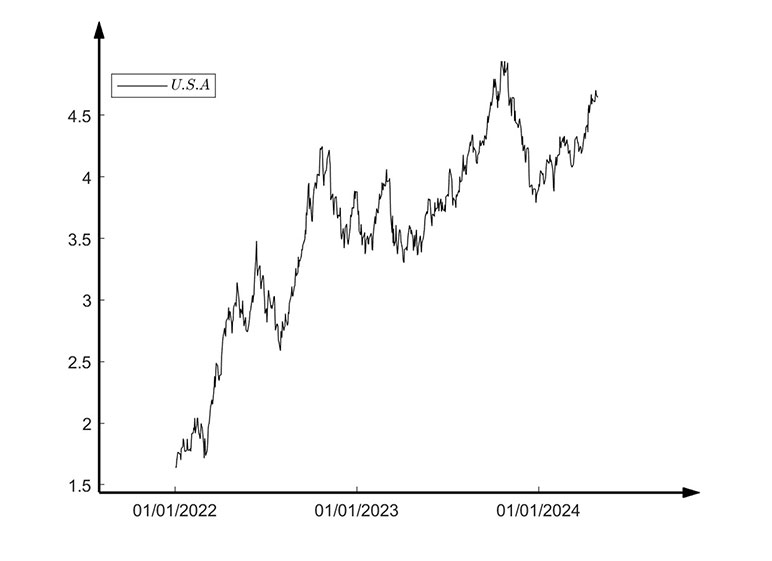
Additionally, significant black swan events, such as global economic crises and geopolitical crises, and the resulting adjustments in macroeconomic policies, often trigger a chain reaction in the life insurance market, leading to a state of violent market fluctuations. During economic crises, investors' confidence is generally shaken, and stock and bond markets fluctuate dramatically, with interest rates potentially rising or falling sharply. The outbreak of geopolitical crises can also increase uncertainty in the capital market, making investors more cautious. After the outbreak of a black swan event, central banks often take targeted monetary and fiscal policies to stabilize the economy. For example, after the 2008 economic crisis, European countries adopted loose monetary policies to stimulate the economy, with the stable level of interest rates dropping from around 4% to 0% or even negative rates. Similarly, in 2023, the U.S. Federal Reserve implemented a tight monetary policy to curb the escalating inflation, causing interest rates to rise rapidly and enter a new state of stability. It can be observed that interest rate levels also change with the transformation of macroeconomic policies. In a sense, this can be likened to a quantum leap where, after being excited, it transitions to a new energy level and stabilizes. (See Figure 7)

Figure 7

U.S. 10-Year Treasury Interest Rates Beginning In 2022

In general, the multi-peak distribution image of the quantum harmonic oscillator can well match the distribution trend of interest rates in most economic scenarios. In the current situation where uncertainty in the global macroeconomic situation is increasing, insurance companies need to study and predict the impact of interest rates on asset-liability management as comprehensively as possible, and flexibly adjust pricing and investment strategies to cope with market changes and ensure their own stable operation and sustainable development. In this process, the probability wave distribution characteristics of the quantum harmonic oscillator in the ground state and excited state can provide us with useful insights, that is, the uncertainty and variability in the market need to be dealt with and managed through a variety of strategies and means. Insurance companies need to gain a deeper insight into the dynamic evolution of interest rates to provide strong support for risk management and strategy formulation. Against the backdrop of increasing macroeconomic uncertainty, the interest rate analysis from the perspective of the quantum harmonic oscillator is of great guiding significance for insurance companies to grasp market trends, optimize asset allocation, and achieve sustainable development.

Statements of fact and opinions expressed herein are those of the individual authors and are not necessarily those of the Society of Actuaries, the newsletter editors, or the respective authors’ employers.